首先,從實際出發,找到問題:

用可莉打冰樹做示範,第一次不帶帽子,用圖中的火傷杯,傷害是5645

第二次不帶杯子,用圖中的攻擊帽,傷害是5149
同樣是46.6%的加成,為何傷害會有明顯差距?
再看下面的情景劇:
①你有1000點基礎攻擊力
②你裝備一個50%攻擊加成的裝備
於是你的攻擊力變成1500,「本次提升」的幅度為(1500/1000)-1=50%
③你再裝備一個50%攻擊加成的裝備
於是你的攻擊力變成2000,「本次提升」的幅度為(2000/1500)-1=33%
也就是說,「第二次提升」相比「第一次提升」的幅度變小了。(注意,並不是提升「沒了」!)
或者說,「上次提升」產生的分母,把「這次提升」的效果給「稀釋」了
OP:若是第二次裝備50%火元素傷害加成的裝備
於是你的傷害變成1500×150%=2250,「本次提升」的幅度為50%
由此得到啟發,把相同的資源投入到不同乘區,將會使你的收益更高。
用「木桶效應」或是「圓面積最大」這樣的常見比喻也很好理解這種現象。
但光定性還不夠,該如何定量呢?
從上面的陳述你應該已經發現,這種現象和「提升後屬性」以及「提升前屬性」有關
於是我們定義:「邊際收益」=「提升後數據」除以「提升前數據」
接下來,邊際收益我會用MRn表示,這裏n就是提升的次數。
(MR本是經濟學的術語,口口相傳的「稀釋」其實被叫做「邊際效應」,也罷,我們刷聖遺物,不就是在做投資嗎?)
然後我們看攻擊力乘區的式子:
攻擊力=白值*(1+百分比加成)
用符號語言就是:AT=A(1+AR)
MR=現在的攻擊力/剛才的攻擊力,要求出來,只要用小學就會的數列就行了:
假設我們每次提升的攻擊力百分比是1.5%
「剛才的攻擊力」為AT1=A
「現在的攻擊力」為AT2=A(1+1.5%)
MR1=(1+1.5%)/1
再來加個1.5%
「剛才的攻擊力」為AT2=A(1+1.5%)
「現在的攻擊力」為AT3=A(1+2*1.5%)
MR2=(1+2*1.5%)/(1+1.5%)
……
以此類推,當第n次提升1.5%攻擊時
MRn=(1+n*1.5%)/(1+(n-1)*1.5%)
好了,這就完事了,我們要的MRn就出來了
同樣道理,依舊是用數列的,很容易就能推出增傷、暴擊、元素精通等等不同乘區的邊際收益表達式。
這裏就直接給大家提供公式吧:
註:n為權重數
1權重=1%暴率=1.5%攻擊=1.5%增傷=1.5%生命=1.875%物傷=1.875%防禦=2%暴傷=6精通
攻擊/增傷:
MRn=1+3/(3n+197)
暴擊屬性:
n∈[1,20]
MRn=1+1/(204+n)
n∈(20,171]
MRn=(20000+(n+30)^2)/(20000+(n+29)^2)
n∈(171,+∞]
MRn=(3+2%(n-170))/(3+2%(n-171))
元素精通:
SPn=25(6n)/9(6n+1400)+1;MRn=SPn/SP(n-1)
物傷
MRn=1+1.875%/(1+(n-1)*1.875%)
然後用exl就能做出曲線了:
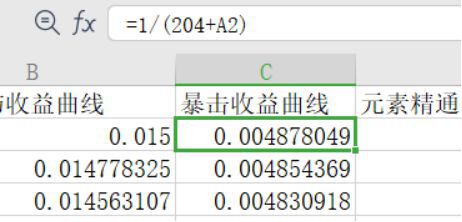
接下來給大家曲線如何看:
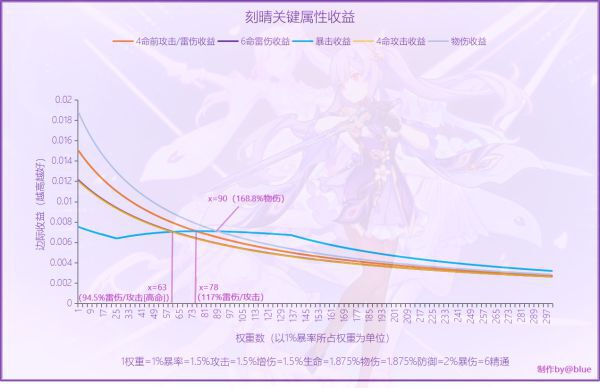
看這張阿晴的曲線圖,首先一下關鍵要素的含義,
①曲線交點:屬性A的「下次提升」收益在此之後低於/高於屬性B
②下方面積:給該屬性投入那麼多資源的總收益
③不同曲線y值相等的點:收益相同時各屬性的權重數
然後根據我們想要解決的問題,從圖中找答案:
①刻晴堆多少攻擊比較好?
通常會和暴擊曲線做對比,看交點,圖中就是117%以後收益低於暴擊,那就可以得出結果,攻擊加成應該堆117%左右
②刻晴堆多少攻擊傷害會低於硬堆暴擊?
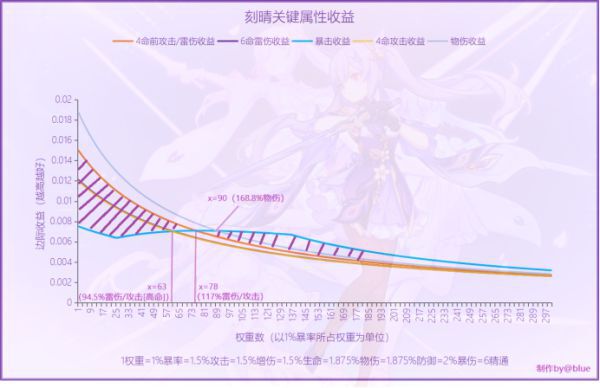
看什麼時候攻擊曲線下方的面積小於暴擊曲線就行,通常不必積分,目測就能知道這種情況在正常游戲中是不會出現的了
③刻晴堆多少攻擊算溢出?
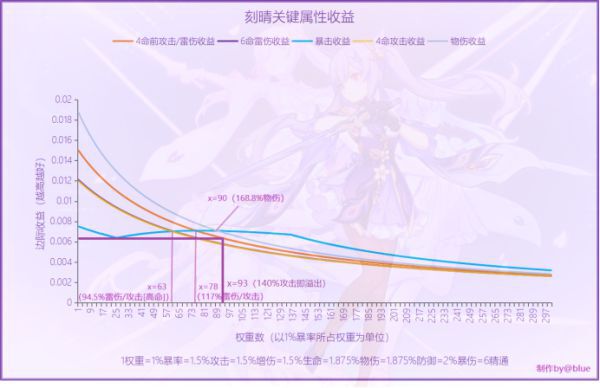
過暴擊曲線左邊的極小值點作平行x軸的直線,看交點,比如圖中就是得到140%攻擊。因為,在此之後,很長一段時間內,對於攻擊乘區「再次提升」的收益總會小於提升暴擊乘區的收益。
④我目前該堆什麼屬性?
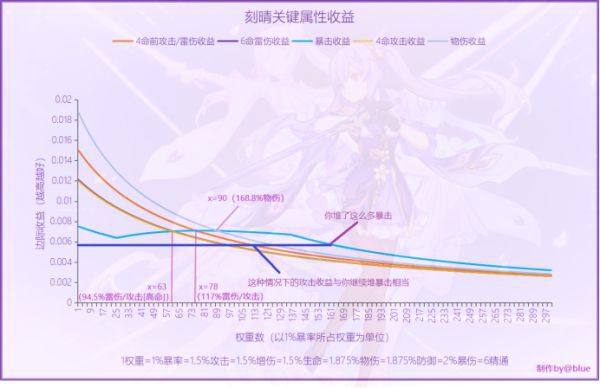
以你目前權重數最高的曲線為起點,作平行x軸的直線,看左方其它曲線的交點,這就代表你應該「回頭」堆哪個屬性。
(但事實上,即使你繼續堆你的,傷害也不會和「絕對最佳方案」差多少,所以最實用的一般是第①問,回答「堆多少比較好」即可)