結論
地軸傾角=0的極限狀況下,緯度從30度開始到75度均可,從30度出頭開始逐漸向高緯度鋪設至60度以入手最大收益。
地軸傾角=a度不為零的情況下,可用角度從兩側都減少a,既緯度從30+a度開始到75-a度均可,從30+a度出頭開始逐漸向高緯度鋪設至60-a度以入手最大收益。
以下是模擬圖以作參考。
一個假設
在開始之前需要一個假設,星球離太陽足夠遠,太陽帆軌道足夠小,此時可認為投射器仰角等於太陽高度角。如果不滿足這兩點投射范圍會更加受限,因此應當盡量設定軌道以滿足此假設。
確定任意地點投射器仰角
為了解決這個問題,首先要解決如何確定某時刻某經緯度地點仰角的問題。
最簡單的問題是地軸傾角為零,正午時確定緯度y下的仰角,如圖
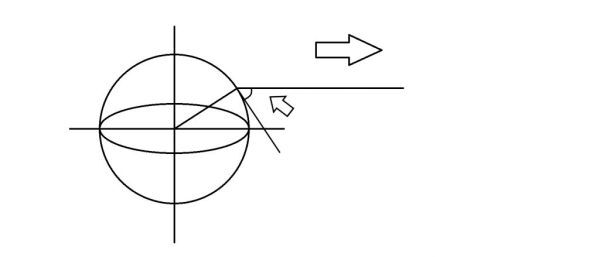
此時大箭頭指向為投射器投射方向,因此小箭頭指向為仰角,由地理知識此角度等於90度減去緯度即90-y度。
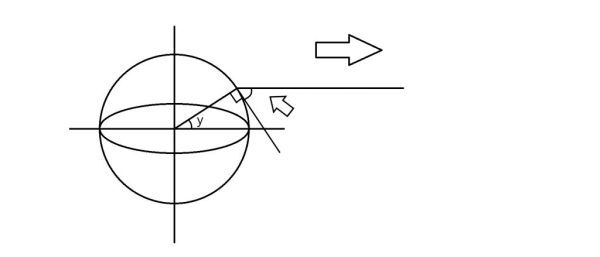
接下來如果不在正午,即太陽直射的地點經度與本地經度存在角度差,那麼如何計算仰角?
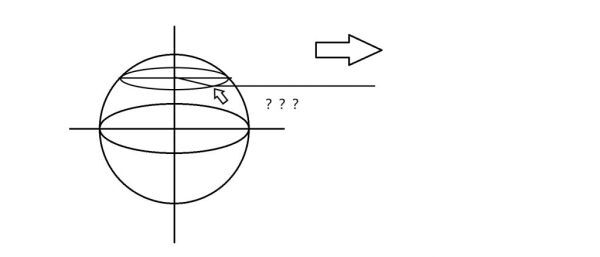
根據地理知識可知此時太陽高度角應為本地到太陽直射點之間的測地線這個圓弧所對應的圓心角的餘角,即90-θ角。
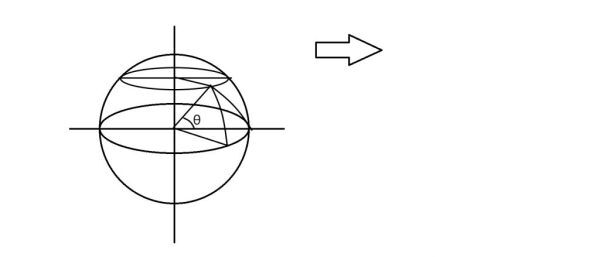
設太陽直射點經度與本地經度差為x度,本地緯度為y度,
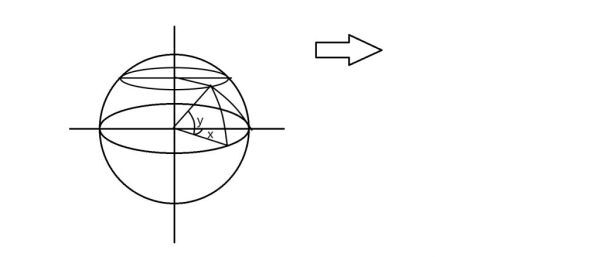
則三者之間滿足換算關系cosθ=cosx*cosy由此可以算出任意經緯度下的仰角。
如何判斷一天以內投射器發射的時間
第二個問題是如何判斷一天以內投射器發射的時間?這個問題相對簡單。由於太陽直射點一天經度改變360度,「本地」相對於太陽直射點的經度差x一天以內隨時間均勻改變360度,因此可以將可投射時間換算為可投射的經度差范圍,同緯度下,經度范圍越大,一天內投射時間越長。
程序模擬
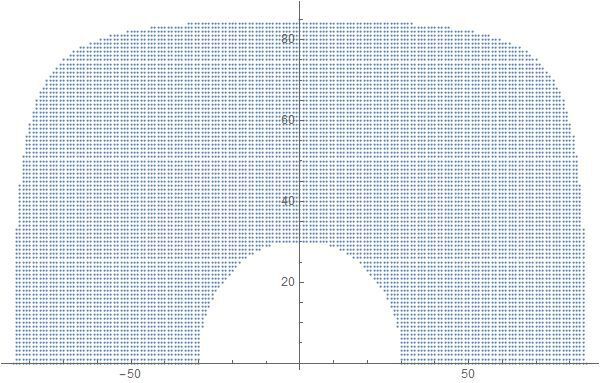
第三個問題就是計算問題,我將星球上面朝太陽的四分之一半球分為經度-90到90,緯度0到90的一系列地點分別判斷每個點是否滿足仰角位於[5,60]之間,程序與結果如下。
製作地點經緯表(精確到1度),判斷仰角,不滿足的設為空
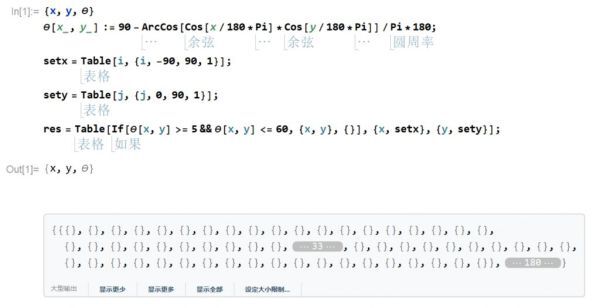
排除空集,剩餘就是滿足條件的地點:橫坐標為經度差,縱坐標為本地緯度
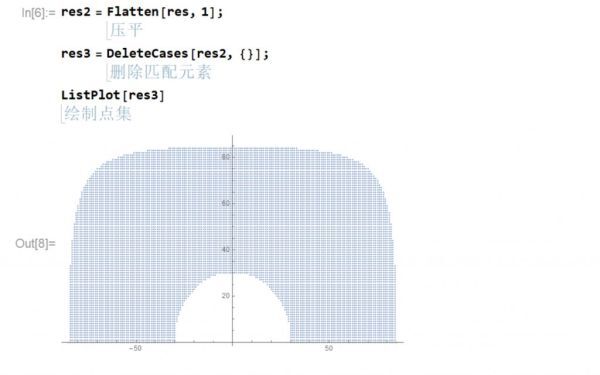
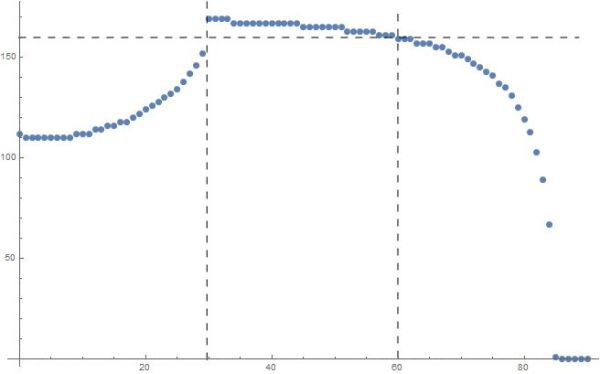
計數,可視化(橫坐標為緯度,縱坐標為合適地點個數,即經度范圍),取出多於160個點的緯度。
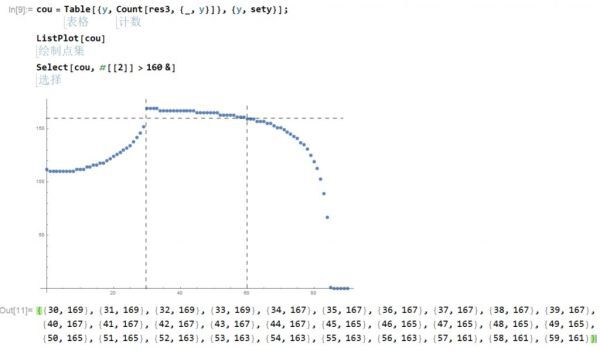
據此可以得到結論:合適的緯度為曲線上最高的部分,即30度以上,約75度以下的部分,其中可用經度范圍大於160度的(即每天投射時間>160/360=4/9)的緯度范圍為30度以上,60度以下。考慮到曲線的形狀右側平緩左側尖銳,從30度的閾值開始逐漸向高緯度鋪設,兩個半球對稱鋪設。
地軸傾角不為零時
最後一個問題是如果地軸傾角不為0,結論會受到什麼影響?這個問題計算起來相對比較復雜,但在小傾角下有一個很簡單的近似:地軸傾角不為零意味着太陽直射位置分享緯度不為0,那麼在冬至時冬季半球所有緯度計算需要加上地軸傾角,合適范圍整體向低緯度偏移;相反此時在夏季半球(夏至)所有緯度計算需要減去地軸傾角,合適范圍整體向高緯度偏移。由於投射器是固定產,我們不得不考慮最差情況,那麼合適緯度范圍需要都向內測偏移地軸傾角即可。