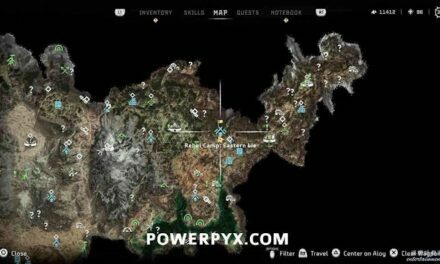
以前做過一個小小的測試,得出了戴森球最大層半徑需要1.35倍的軌道半徑來使被包行星的所有點射線強度打到100%
同時提出了一個假說來計算戴森球外部行星上能維持100%射線強度的范圍
可惜的是假說經過我的測試,在一些距離較遠的行星上有很大的偏差
於是使出了最終手段: 解包
結論
1 不要用戴森雲軌道中繼,直接戴森球半徑拉滿
2 透鏡效果為直接加算,如果在太陽背面也能拉到100%那麼任何地方都可以通過透鏡拉到100%
計算過程
計算基本信息如下
a. 恆星向量v1(大小為1, 只用於確定方向)
b. 發射器位置分享向量v2(大小為1)
c. 戴森球最大層半徑與行星軌道半徑的比值k
d. 電離層增強系數i
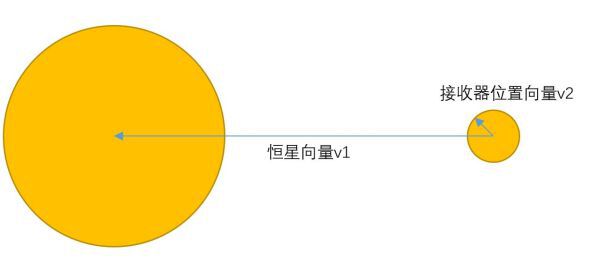
射線強度為
strenth = {(v1 . v2) + k * 0.8 + i} * 6 + 0.5
v1.v2
為兩個單位向量的內積, 接收器擺放的位置分享會影響這個值
比如在地軸傾角很小的行星的極點的話,這個值約等於0
而完全在太陽背面的時候,這個值為-1
k
基本上就是戴森球與行星軌道的半徑比, 戴森球半徑也就是解包里的grossradius,如果是戴森球殼的話會直接按最大層半徑算,
結果就是之前網友提出的虛空層也能起作用這個很詭異的結果
戴森雲的時候 grossradius = 最大軌道半徑 * 0.75 + 平均軌道半徑 * 0.25
所以戴森雲在計算上不如虛空球殼有利
i
也就是透鏡的效果系數,沒放就是0, 這個的具體計算放在後面
這個射線強度值會被限制在0 – 100%之間
很神奇吧。。並沒有什麼復雜的計算
和之前的需要1.35倍的半徑比使球內行星全球接收的結論比較下,基本吻合, 正確的數值為1.354167
引力透鏡的效果
引力透鏡的效果 i由電離層高度和行星半徑算出,而這個效果是直接加算上去的
電離層高度h = (未知, 與行星的類型有關,我實在是在代碼里找不到。。。)
與行星半徑r = 200
設電離層有效半徑R = r + h * 0.6
i = sqrt(R^2 – r^2) / R
也就是說會用電離層有效半徑 R為斜邊和行星半徑r 計算sine值
帶來的具體強度增幅見下圖
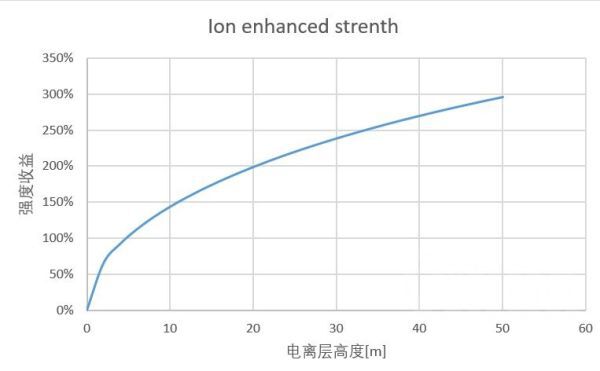
3 射線接收器擺放位置分享
那麼球外的射線接收器該擺哪裏呢
首先 首選100%強度的位置分享
比如你的行星軌道半徑40000m,戴森球半徑20000m,
那麼40000/20000 = 2在下圖中可以知道 71.5度以上是首選位置分享
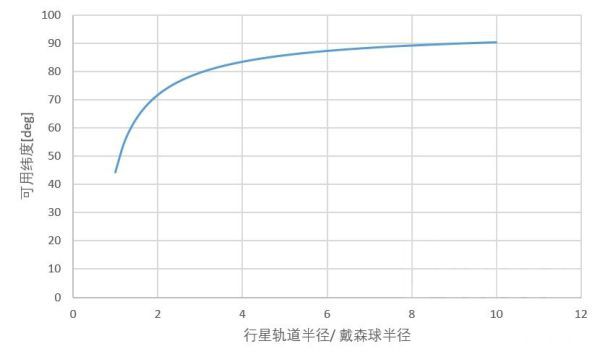
次選位置分享要求能夠維持暖機
接收器暖機要求75%的強度。
定標准為75%以上的話
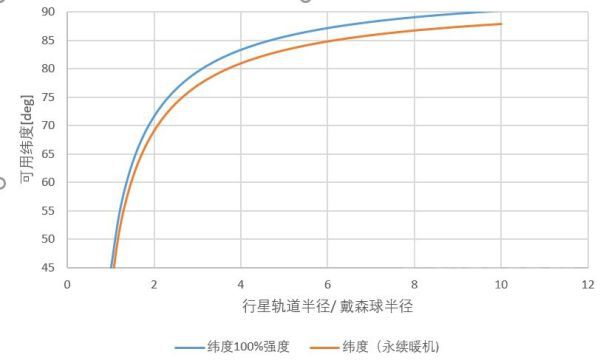
同條件下多了 2.5度,大概可以多擺一圈?