本文適合有以下問題的玩家
我就是要造個高高大大的軌道,可為什麼彈射器老是報警?
我有個潮汐鎖定的星球,該在哪部署彈射器?
我沒有潮汐鎖定的星球,該在哪部署彈射器?
結論
彈射器的射擊目標點會隨行星公轉而變化,一年中不同時間段發射效率可能不一樣。
避免在衛星上發射太陽帆。
太陽帆軌道半徑R與行星軌道半徑r之比(R/r)越大,傾角越接近直角,發射效率越低。即使在潮汐鎖定星球上也會縮小全時段可發射范圍。所以離恆星越遠的星球在發射上越有優勢,選擇發射星球的優先級一般是潮汐鎖定>遠日行星>其它。
在潮汐鎖定星球上,避開正午經線東西30°和南北緯30°之內的范圍,打接近垂直的軌道就向低緯度10點和14點(正午12點)左右的區域佈置,打接近水平的軌道可以隨意佈置。R/r越大,全時段可發射范圍越小,要求越嚴格。同時太陽帆軌道傾角增大會使發射范圍整體西移。赤道上正午經線東西30°-60°的范圍是黃金位置分享,幾乎能打所有軌道。
在有明顯晝夜交替的星球上,R/r越小,優勢區域緯度越高,R/r越大,優勢區域的緯度越低。小半徑軌道(R/r<0.3)佈置在20°以上的中緯度地區,大半徑(R/r>0.5)佈置在赤道南北。
如果可以,盡量設計軌道使得北半球夏季打北天球目標點,冬季打南天球目標點。
前置知識
彈射器基礎
彈射器的發射障礙主要有兩個:俯仰限制和目標遮擋。
如果射擊目標點的仰角不在5°到60°范圍內就會受到俯仰限制。
如果與目標點的連線穿過其它天體周邊一定范圍內(中心向外半徑+120米)則形成目標遮擋。這樣就產生了第一個原則:盡量避免在衛星上放彈射器。
約定
1.黃道平面:指默認的1號軌道所在平面;
2.全局坐標系:指以恆星為原點、升交角0°經度為x軸、90°經度為y軸、垂直於黃道平面向北的向量為z軸的坐標系,如下圖。如果無特殊均使用全局坐標。
3.緯度:如果無特別,緯度一般南緯取負、北緯取正,經度范圍0°-360°。
4.軌道傾角越高,是指太陽帆軌道傾角越接近90°(越垂直於黃道面);軌道傾角越大,是指太陽帆軌道傾角越接近180°。
5.重要符號表
| 符號 | 含義 | 符號 | 含義 | 符號 | 含義 | 符號 | 含義 | 符號 | 含義 |
| T | 行星公轉周期 | K | 行星自轉周期 | θ | 太陽帆軌道傾角 | η | 太陽帆升交角經度 | R | 太陽帆軌道半徑 |
| α | 軌道彈射器緯度 | β | 彈射器所在經度與某一給定經度的差 | γ | 行星地軸傾角 | ω | 行星公轉相位,ω=2πt/T | r | 行星軌道半徑 |
| τ | 彈射器目標點與彈射器天頂方向的夾角 | ζ | 目標點與太陽在彈射器處的視向張角 | δ | 太陽直射點緯度 | φ | 彈射器處的太陽直射點高度角 | k | 行星公轉周期與自轉周期之比T/K |
| n | 太陽帆軌道面法向向量 | i | 彈射器處的天頂方向向量 | T(出現在向量中或表示點的時候) | 目標點位置分享 | P | 行星位置分享 | E | 彈射器位置分享 |
射擊目標點
太陽帆射擊的目標點在軌道上不是固定的,取決於兩個因素:太陽帆軌道面法向和彈射器的全局坐標。
目標點一定在軌道上,其方向是軌道面法向與彈射器位置分享向量的向量積。
太陽帆軌道面法向
太陽帆軌道的軌道傾角θ(0°≤θ≤180°)和升交角經度η(0°≤η≤360°)決定了軌道面的法線方向。
游戲預置的1號軌道傾角0°、升交角經度0°,其法向就是z軸正向(0,0,1)。玩家自定義的軌道法向按如下方式確定:
先將向量(0,0,1)繞x軸旋轉θ,再繞z軸旋轉η。
因此軌道面法向n=(sinθsinη,-sinθcosη,cosθ)。
推導過程:
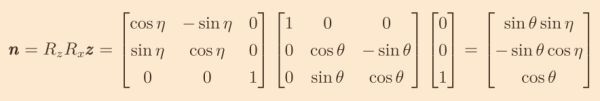
彈射器的全局坐標
因為彈射器在行星上,首先需要確定的是行星坐標,行星位置分享由行星在軌道上的相位ω(ω=2πt/T,T為公轉周期,t為當前時刻)、公轉軌道傾角λ、公轉軌道與黃道平面交點的經度μ、行星軌道的半徑r決定。
行星坐標P=r(cosμcosω-cosλsinμsinω,sinμcosω+cosλcosμsinω,sinλsinω)。
推導過程:

而彈射器在行星上的坐標則與彈射器所在緯度α(南緯為負,北緯為正)、天球經度2πt/K+β= kω+β(*)(K為自轉周期,k=T/K是行星公轉周期與自轉周期之比,如果反向自轉則k=-T/K)、行星的地軸偏角γ、行星自身的半徑a有關。
β是初始時刻彈射器經度與x軸的經度差(向東增加),雖然β一般很難確定,但問題其實不大。如果行星不是軌道共振星,那麼β可以忽略,因為往往K遠小於T,可以認為一個晝夜間行星位置分享沒變,但天球經度已經取遍0~360°,β帶來的影響很小。潮汐鎖定星的β則非常好確定:可以認為正是其子夜經線(永夜面中心經線)的經度。
實際上在游戲裏彈射器自身的高度對這個坐標也是有影響的,但是因為量級太小這裏不考慮。所以彈射器在行星自身的局部坐標系上的坐標為(r(cosμcosω-cosλsinμsinω)+a(cosαcosγcos(kω+β)+sinαsinγ),r(sinμcosω+cosλcosμsinω)+a cosαsin(kω+β),rsinλsinω+a(sinαcosγ-cosαsinγcos(kω+β)))。
推導過程:

目標點T的位置分享滿足OT=n×OE/| n×OE |*R,R為太陽帆軌道的半徑。
復雜的表達式預示着這個問題的高精度的定量解只能通過程序為每個玩家的場景去算(暗示MOD),我們在這裏必須簡化一下。
簡化模型和目標點的天頂角
簡化模型
來看看能夠忽略掉哪些影響因素。
第一個是行星的軌道傾角λ,這個傾角一般都非常小(<10°),導致行星的縱坐標一般不會超過±0.003r的范圍。所以可以認為行星的公轉軌道就在黃道平面上。而如果軌道傾角λ=0,那麼軌道與黃道平面交點經度μ也就沒有實際意義了,取任何值都行,可以一樣取為0。於是行星位置分享就被簡化為(cosω,sinω,0)。
第二個是彈射器位置分享與行星中心的相對位移PE。根據設定,行星半徑|PE|=200m,但即使距離恆星最近的行星其軌道半徑也是近萬米,常見的軌道都在0.5AU以上,相差兩個量級。所以對目標點位置分享影響最大的是行星自身的位置分享,彈射器在行星上的具體位置分享影響非常弱:OT/R=n×(OP+PE)/|OP+PE|=n×OP/|OP+PE|+n×PE/|OP+PE|,|PE|遠小於|OP|時,|OP+PE|→|OP|,n×PE/|OP+PE|=|PE|/ |OP+PE|→0,所以可以直接使用n×OP來計算目標點的方向向量。
簡化後的目標點為:
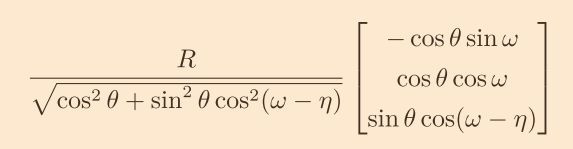
目標點有兩個值得討論的地方:
1.顯然目標點的位置分享是隨着行星的公轉(由ω決定具體位置分享)而變化的。
但這種變化並非勻速——軌道傾角越高,在越靠近黃道平面的部分動得越快,也就是一年中的大部分時間目標點都會位於軌道距黃道平面較遠的那部分。極端情形是90°傾角的軌道(也就是垂直於黃道平面),此軌道全年的目標點都在上下兩個端點附近,行星過升交角經度時切換。
2.目標點的全軌道變化使得高緯度地區的彈射器有時會陷入麻煩。
例如如果是北半球的高緯度彈射器,可能無法向黃道平面以下較遠的目標點發射,導致其有相當一部分時間都處於啞火狀態。特別是如果軌道安排得很尷尬,導致北半球的夏季目標點在黃道平面以下,冬季在黃道平面以上,會嚴重影響彈射器的工作效率,地軸傾角較小的行星則比較省心。
目標點表達式前面帶的根號很麻煩,可以將前面的整個系數記為M。
目標點的天頂角
下面來計算天頂角τ(彈射器對目標點的朝向與彈射器正頭頂方向的夾角),天頂角的餘角就是目標點的仰角,因此彈射器的可發射范圍是30°<τ<85°的時候。
得益於游戲將行星簡化為一個完美球形(而不是方形),彈射器自身的天頂方向單位向量很容易確定:各分量就等於彈射器本地坐標除以行星半徑a,在彈射器處,目標點的視向向量可以近似為PT=OT-OP,即(-Mcosθsinω-rcosω,Mcosθcosω-rsinω,Msinθcos(ω-η)),該向量模長平方為R²+r²。

從而目標點天頂角τ滿足cosτ=PT·i/|PT|。得到
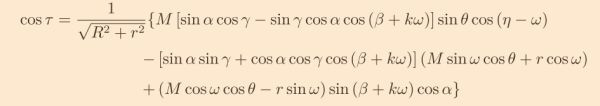
這個表達式包含兩項運動而且帶有根式,仍然不好做解析的分析,所以先從簡單類型的行星搞起。
潮汐鎖定行星
在現實中,潮汐鎖定並不嚴格等同於永晝永夜。理論上行星自轉角速度在垂直於軌道平面上的分量等於公轉角速度就可以形成潮汐鎖定,但是因為地軸傾角、軌道傾角、軌道形狀等因素形成的天平動會導致仍然有一部分區域出現晝夜交替(例如月球,地球上的實際可見范圍大於50%)。不過游戲裏採用了一種相當粗暴的簡化:所有行星公轉軌道都是正圓,當確定該行星為潮汐鎖定時,行星公轉周期等於自轉周期,同時其地軸傾角會變得非常小(直接在預設的隨機值上乘了個0.01)。所以對於游戲裏的潮汐鎖定星球還可以進一步簡化:公轉周期與自轉周期之比k=1,地軸傾角γ=0。
如此前述天頂角可化簡為:
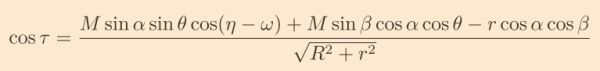
此式可以給出幾個結論:
1.潮汐鎖定星球彈射目標點的天頂角與自轉無直接關聯(雖然這是一句不需要看公式也想得到的廢話)。
2.分子分母同除以r並令R/r→0則可以得到小半徑太陽帆軌道近似下的結果。注意因為永晝面的β范圍是[90°,270°],所以-rcosαcosβ在永晝面的實際符號是正。
3.θ=0或α=0時,天頂角與行星公轉無關。也就是對位於黃道面上的軌道或者赤道上的彈射器,某一刻可以彈射的位置分享永遠可以彈射,此時目標點、彈射器處於相對靜止。
4.求導可發現這是一個隨cos(ω-η)單調的函數,在ω=η和ω=η+180°時取到極值,因此潮汐鎖定星球上全時段可發射的判據是
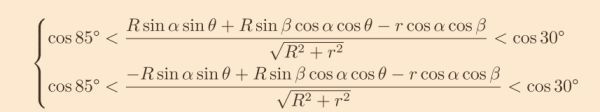
天頂角餘弦的極差是|2Rsinαsinθ|,其它條件不變時,增高緯度、拉大太陽帆的軌道半徑、拉高軌道傾角都會縮小全時段可發射范圍。測試彈射器時可以優先測試大半徑高傾角的軌道。
5.可以據第4條繪制全時段可發射的點的范圍:
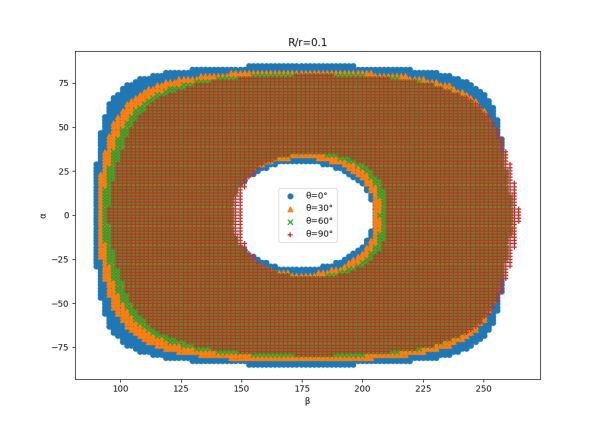
當R/r較小時可發射范圍則非常大,除正午經線東西25°和南北緯25°以內的范圍外其它大部分區域都能實現全時段發射。
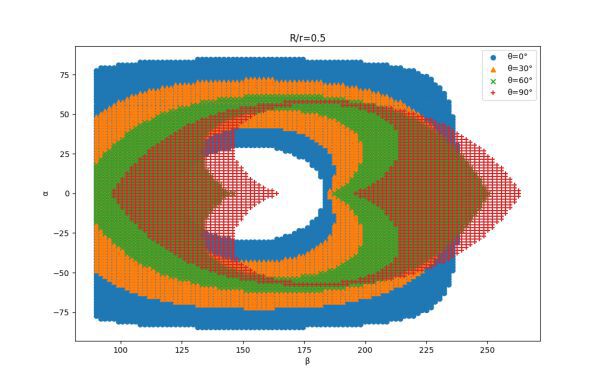
當R/r變大時發射范圍便會縮小,圖中明顯可見當|θ-90°|越小時全時段發射范圍越是向低緯度地區收縮,同時隨着θ趨向180°整個區域逐漸西移。因此一般的規則是高傾角軌道選擇較低緯度靠近晨昏線的位置分享佈置彈射器,低傾角軌道可以選擇高緯度的位置分享。
6.接上條,隨着太陽帆軌道傾角接近180°,全時段區域整體會向西移動,所以如果一個軌道在子夜經線+135°的地方不好打,不妨試試子夜經線+225°的地方。
總體而言,在潮汐鎖定星的中低緯地區沿着緯線佈置一條彈射器腰帶可能是不錯的選擇,保證絕大多數軌道都有合適的彈射器位置分享打。
一般行星
直接從一般行星的天頂角表達式入手很難,但是我們可以先不直接考慮天頂角,而是去求目標點和恆星在彈射器處的視向關系。
其實從目標點的計算中可以看到。目標點、恆星、行星之間構成了一個直角三角形,在行星處的夾角為arctan(R/r),這也可以說是在彈射器處恆星與目標點的視張角(彈射器的具體位置分享對三角形的影響很小)。如果R遠小於r,那麼自然退回到以恆星高度角代替目標點天頂角餘角的情形中去。OT=OP+PT=(-Mcosθsinω,Mcosθcosω,Msinθcos(ω-η)),該向量的模長固定。故在彈射器看來,目標點一年的視運動也是一個圍繞恆星的圓周運動,在一天中隨着恆星一起升落。彈射器視運動的方向與軌道面法向有關。
恆星的視運動
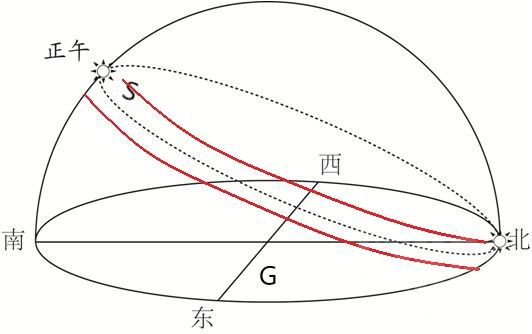
恆星的運動軌跡是平面S與天球的交,地平面為G,南北-東西線交點是觀測點。圖中虛線所示為北半球極晝區域的恆星視運動(這個視運動是勻速的)。向赤道區域走北側軌跡會下沉,南側上升,恆星位於地平面以下時就是夜晚。
目標點的視運動區域必定在兩條紅線之間。
恆星高度角φ取決於當地緯度α和恆星直射點緯度δ(同樣是北緯正南緯負),滿足sinφ=sinαsinδ-cosαcosδcos(2πt/K)。
估計可用時間的下限
![]()
而恆星高度角φ與目標點天頂角τ的關系為90°-τ-ζ≤φ≤90°-τ+ζ,ζ=arctan(R/r),30°≤τ≤85°的充分(不必要)條件是min(5°+ζ,60°-ζ)≤φ≤max(5°+ζ,60°-ζ)。我們的問題是如何選取α使得滿足以下判據的t的區間Δt最長。
求解Δt得到的是一個還算齊整但也不好算的表達式。
Δt的推導:

形式雖然仍對解析不友好,但是到這裏已經可以做下數值求解了。
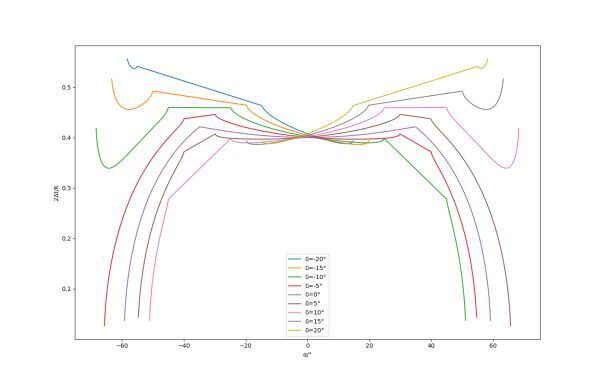
取a=0.2,b=0.82(對應ζ=5°),可以入手下圖:
而如果對應ζ=30°,則有:
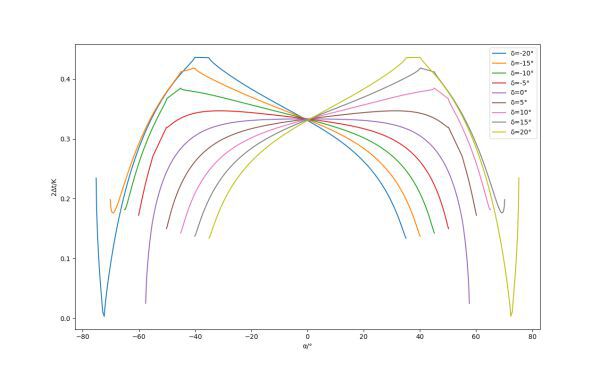
縱坐標已經轉化為一天中可發射時間與自轉周期之比。
需要的是兩圖最上方和最下面的曲線兩端翹起部分是因為在該區間下反餘弦函數內的分母會急劇減小,計算機不會算極限導致數值膨脹,實際趨勢是向下的。
從圖中可見:
1.恆星直射角變化的影響是將該曲線進行旋轉。也就是說,地軸傾角越大,該曲線一年中越能「顛來倒去」,所以大地軸傾角(>20°)的行星可以考慮在南北對稱佈置彈射器,或者扔在全年不虧的低緯度地區(<20°)。
2.在任一緯度處畫一條豎線,與各曲線的交點可以看作是該緯度上彈射器發射佔比在一年中的變化。可見全年都有較大發射范圍的優勢區域隨太陽帆軌道半徑與行星軌道半徑R/r之比的增大而向低緯度收縮。小半徑軌道優勢區域在20°-40°的中緯度,大半徑軌道優勢區域則是南北緯10°之內。
以上結論有一點要注意:上述討論的發射佔比是「下限」,實際根據軌道形態、升交角經度與行星冬夏季節的關系在一些地方可以產生額外的發射窗口。




