先放結論
1.暴擊屬性在雙暴約70%/140%之前稀釋程度逐漸減小。
2.暴擊屬性在雙暴約70%/140%以後稀釋程度開始增大。
3.攻擊加成稀釋現象一開始較為輕,但最終越來越嚴重。
4.在120%攻擊力加成以後,暴擊屬性的稀釋程度將小於攻擊加成,且一直保持這個規律。
實際應用建議
1.先堆到攻擊力(綠值/白值)約120%
2.然後開始堆暴擊屬性,盡可能使你的實際(暴率:暴擊)接近1:2
3.堆到滿暴,也就是雙暴100/200以後,只堆暴傷即可
(關於第3條建議在本帖結尾處有詳細)
註:像冰套被動提供的20%暴率、陣容雙火提供的25%攻擊、刻晴大招提供的15%暴率,此類相對穩定的收益均可納入計算,不局限於面板值
稀釋的定義:邊際收益小於1.5%即存在稀釋,小於1.5%的程度代表稀釋程度。
如此定義的理由:
以下曲線都是按每投入1個單位權重所入手的邊際收益點陣擬合而成的,而一般習慣性地將1%暴擊率所佔權重作為單位權重,此時1單位權重對應1.5%攻擊力加成,再由攻擊力曲線無限靠近0時,邊際收益的極限為1.5%,與1.5%攻擊力加成正好吻合,所故以此作為判斷標准。
即使暴擊和攻擊是不同乘區,投入的權重是可以按比例去定義的,所以這樣取1.5%為標准值就不會受到不同乘區的限制。
攻擊力稀釋規律
准備工作
首先定義:
AR=(綠字/白字),即攻擊力百分比加成,初始為0
MR=(提升後攻擊力)/(提升前攻擊力),即實際提升量
單位權重:相當於1%暴擊率所佔權重,攻擊力單位權重=1.5%攻擊力加成
ar:每次提升的百分比攻擊力
n:提升次數
已知:
攻擊力=白值x(1+AR)
故研究稀釋規律只需研究(1+AR)即可
推導詳細
採用數列得出規律:
第1次提升攻擊力ar:
AR1=1+ar;MR1=(1+ar)/1=1+ar
第2次
AR2=1+2ar;MR2=(1+2ar)/(1+ar)=1+ar/(1+ar)
第3次
AR3=1+3ar;MR3=(1+3ar)/(1+2ar)=1+ar/(1+2ar)
……
第n次
ARn=1+nar;MRn=(1+nar)/(1+(n-1)ar)=1+ar/(1+(n-1)ar)
令ar取單位權重,即ar=1.5%
得:MRn=1+3/(3n+197)
實際增長的百分比就是MRn-1的值
初步結果
用exl製作MRn-1=3/(3n+197)的圖像:
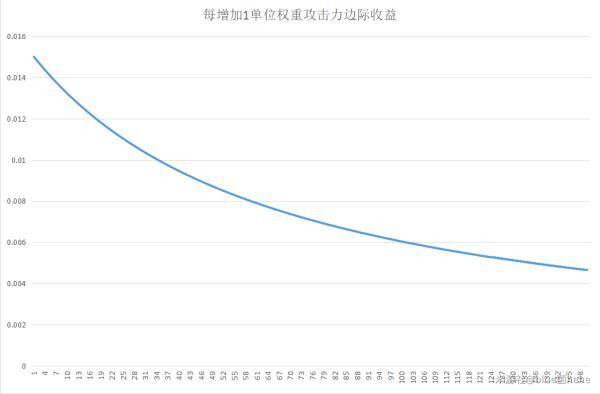
可以發現,攻擊力的稀釋程度越來越大,但最終趨於平緩。
暴擊屬性稀釋規律
准備工作
首先定義:
P為暴擊幾率
CD為暴擊傷害
CR=(1+P*CD),即暴擊收益
MR=(提升後暴擊收益)/(提升前暴擊收益),即實際提升量
單位權重:相當於1%暴擊率所佔權重,攻擊力單位權重=1.5%攻擊力加成
p:每次提升的暴擊率
cd:每次提升的暴擊傷害
n:提升次數
推導過程
依舊是採用數列得出規律:
按照暴率:暴傷=1:2提升
第1次:
P1=p/2;CD1=p;CR1=1+P1*CD1=1+(p^2)/2
第2次:
P2=p;CD2=2p;CR2=1+P2*CD2=1+((2p)^2)/2
第3次:
P3=(3/2)p;CD3=3p;CR3=1+P3*CD3=1+((3p)^2)/2
……
第n次:
Pn=(n/2)p;CDn=np;CRn=1+Pn*CDn=1+((np)^2)/2
於是得出了CRn=1+((np)^2)/2
MRn=CRn/CR(n-1)=(2+(np)^2)/(2+((n-1)p)^2)
令p=0.5%;cd=1%以保證每次提升總共一個單位權重
得MRn=(20000+n^2)/(20000+(n-1)^2)
實際增長的百分比就是MRn-1的值
這樣僅僅得出了不考慮初始值,不考慮滿暴的表達式,接下來將以該表達式為起點進行修正:
已知初始暴率=5%,初始暴傷=50%
n∈[1,20]時,只堆暴率
得到Pn=5%+np;CDn=50%;CRn=1+50%*(5%+np)
令p=1%,得到MRn=CRn/CR(n-1)=1+1/(204+n)
n∈(20,171]時,按1:2堆暴率暴傷,圖像正好是原始曲線向-x方向平移30個單位得到的,所以只需在原始表達式中將n用(n+30)替代
得到MRn=(20000+(n+30)^2)/(20000+(n+29)^2)
n∈(171,+∞]時,暴擊率達到滿暴100%
此時CRn=1+2((n+30)-200)p
MRn=CRn/CR(n-1)
代入p=1%後得到:
MRn=(3+2%(n-170))/(3+2%(n-171))
初步結果
用exl製作MRn-1=(20000+n^2)/(20000+(n-1)^2)-1的圖像:
(最原始的曲線)
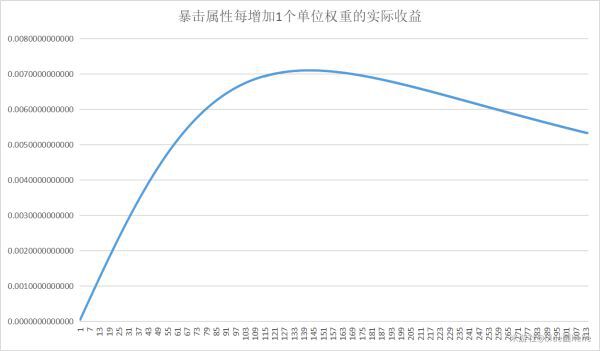
用exl製作分段函數圖像:
MRn-1=1/(204+n) n∈[1,20](20000+(n+30)^2)/(20000+(n+29)^2)-1 n∈(20,171](3+2%(n-170))/(3+2%(n-171)) n∈(171,+∞]
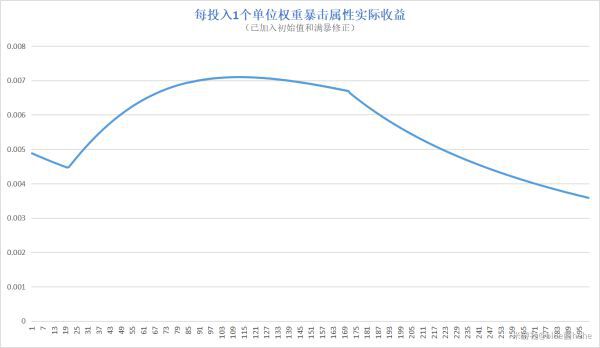
可以發現,在曲線總權重到20之前,稀釋程度逐漸增大,曲線總權重110左右時出現極值點,對應實際面板為70%暴率140%暴傷,在此之前堆暴擊屬性稀釋程度逐漸減小,在此之後又慢慢增大,到滿暴以後發生突變,從平緩到陡峭。
總體比較:
將2條曲線放入同一坐標系中:
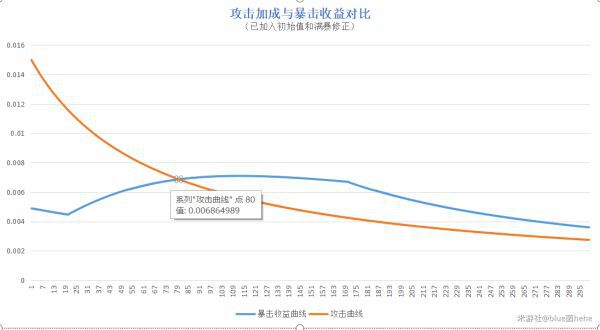
圖中關鍵數值點:
1.交點(x=80,y=0.006865),對應:攻擊力120%;對應雙暴55/110
2.暴擊曲線數值再次等於0.006865時,x約為154,對應雙暴92/184
3.暴擊曲線極值點近似為(x=112,y=0.007096),對應雙暴71/142
4.暴擊曲線前後2個分段點橫坐標(x=20;x=170)對應雙暴25/50和100/200
由此得出結論
1.暴擊屬性在雙暴25/50之前會出現短暫的稀釋增加 ,而接下來一直到71/141稀釋程度都會有所下降,71/142以後稀釋程度再次提高,但相比攻擊力加成的稀釋現象會輕一些。
2.雙暴92/184以後,再次堆暴擊屬性的邊際收益會低於回頭補攻擊加成,所以接下來要按比例同時堆。(具體關系還在摸索,但不是簡單的按每次各堆相同權重就行)
3.攻擊力一開始稀釋程度較小,最終趨於平緩,但最後稀釋現象會比暴擊屬性嚴重。
補上更大取值范圍的圖像:
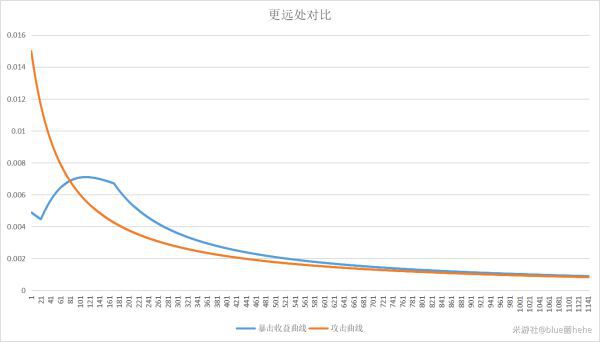
結論都是對於一般角色而言的,對於諾艾爾、阿貝多、鍾離這樣的特殊屬性加成的角色不一定適用,突破加暴傷這樣的角色也會出現一些誤差,但誤差肯定在能接受的范圍內,放心參考即可。